简介
离散化与稠密化是机器学习领域的两个重要概念,虽然不是互逆的概念,但是二者却有共通之处。
离散化的本质是将连续型数据分段,而稠密化的本质是降低表征维度。
前者是在单一维度特征内部进行”降维“,而后者是在不同特征之间进行实打实的降维。
下面对这两个概念分别进行介绍。
离散化
有些数据挖掘算法,特别是某些分类算法(如朴素贝叶斯),要求数据是分类属性形式(类别型属性),这样常常需要将连续属性变换成分类属性。
另外,如果一个分类属性(或特征)具有大量不同值,或者某些值出现不频繁,则对于某些数据挖掘任务,通过合并某些值减少类别的数目可能是有益的,具体优点分析如下:
- 避免one-hot场景下频繁扩充维度,并且容易造成维度不匹配的问题
- 离散化后的特征对异常数据有很强的鲁棒性,比如我们可以把异常数据归并到一类里面,给一个统一的值,避免对结果造成过大的干扰。
- 离散化之后可以有效的进行特征交叉,提升模型表达能力
- 减轻过拟合风险,提升模型稳定性。比如31岁和30岁并没有太大的区别,不能因为长了一岁就对结果有了明显的影响;并且对于逻辑回归这种模型来说,离散化会减少参数量,显式的简化了模型,减轻了过拟合。
无监督离散化
- 等距离散化
- 等频离散化
- 基于聚类分析的离散化(先聚类,再合并(自底向上)或分裂(自顶向下),达到预定的簇个数)
- 基于正态3σ的离散化
有监督离散化
- 基于信息增益的离散化(自顶向下)
- 基于卡方的离散化(自底向上,根据不同区间的类分布相似度进行聚合,相似度越高,卡方值越小)
小结
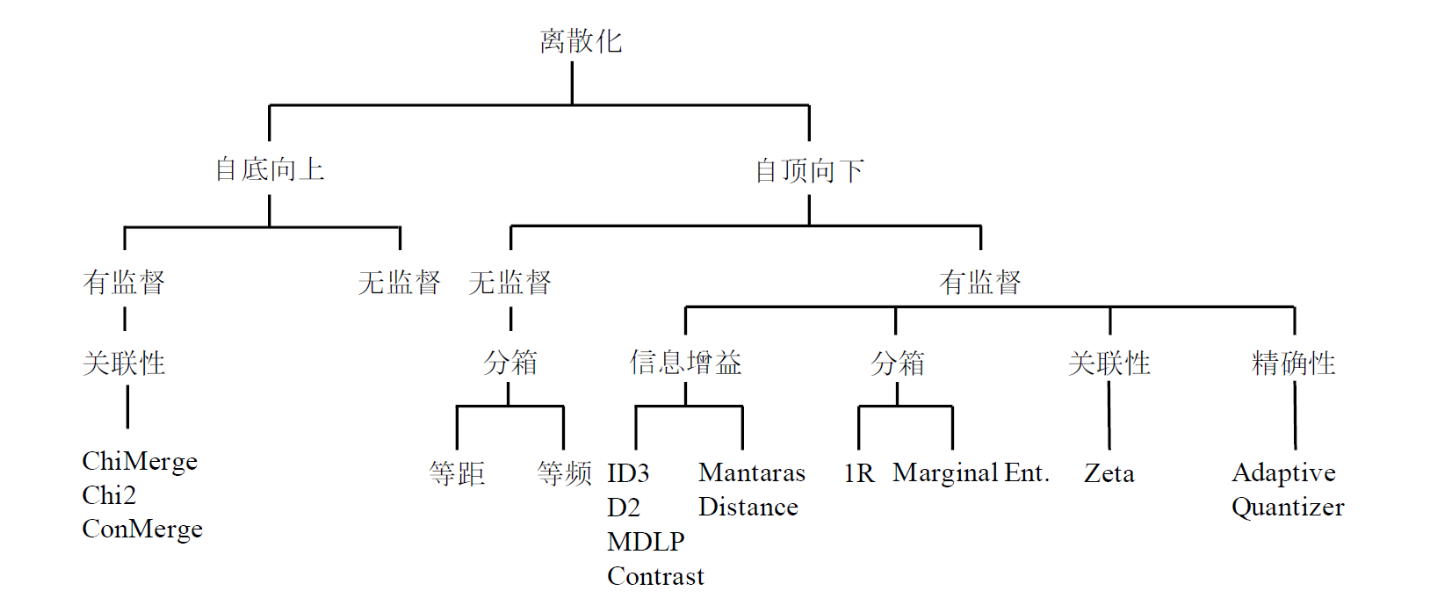
稠密化
稠密化在深度学习中有一个更常见的称呼——Embedding。一般来说,我们稠密化的对象是稀疏向量,最常见的是one-hot向量。
举一个简单的例子,在NLP中,我们会遇到多种one-hot向量,比如单词的原始表征、tf-idf表征等等,动辄就几十万维。对于这种表征,如果不进行稠密化,对空间复杂度和时间复杂度都是一个很大的考验。
将其稠密化为embedding之后,起码有如下优势:
- 可以在不丢失信息的情况下实现降维,降低空间复杂度和时间复杂度。(众所周知,3维就可以表征8个状态,但是one-hot需要8维)
- 可以在嵌入空间赋予向量物理意义,使得向量之间可以有效的比较相似性,比如常见的在嵌入空间做余弦相似度。
- 避免one-hot的扩充和维度不对应问题
具体做embedding的方法,目前已经多不胜数。最为经典的还是word2vec系列,并且近几年深度学习推荐系统的发展更是推进了embedding方法的扩展,graph embedding已经在推荐系统领域得到了广泛应用,在graph中可以灵活的添加side-information,甚至直接结合knowledge-graph,使得embedding的语义信息越来越丰富。