数据类型
表格数据
行为对象(元组、数据点、实例、样本均为相同概念),列为属性
属性
维、特征、变量、属性均为相同概念
数据类型
- 名义型
- 布尔型
- 等级型
- 数值型
数据的基本统计信息
统计中心趋势和离散程度:
- 均值:算数均值、加权均值
- 中位数(median)
- 众数(mode)
- 对于适度倾斜的单峰曲线,有经验公式:mean - mode = 3 * (mean - median)
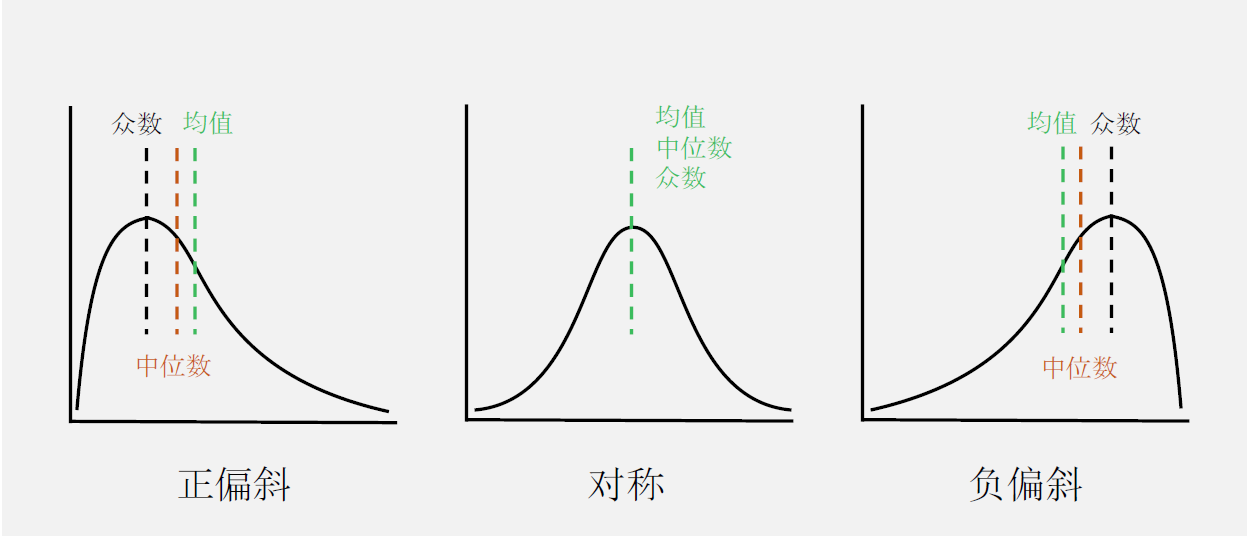
- 分位数(Quantile):x为数据集中的数,如果数据集中百分之K的数都不大于x,则称x为数据集的K分位数
- 上四分位数(Q3-75% quentile)
- 下四分位数(Q1-25% quentile)
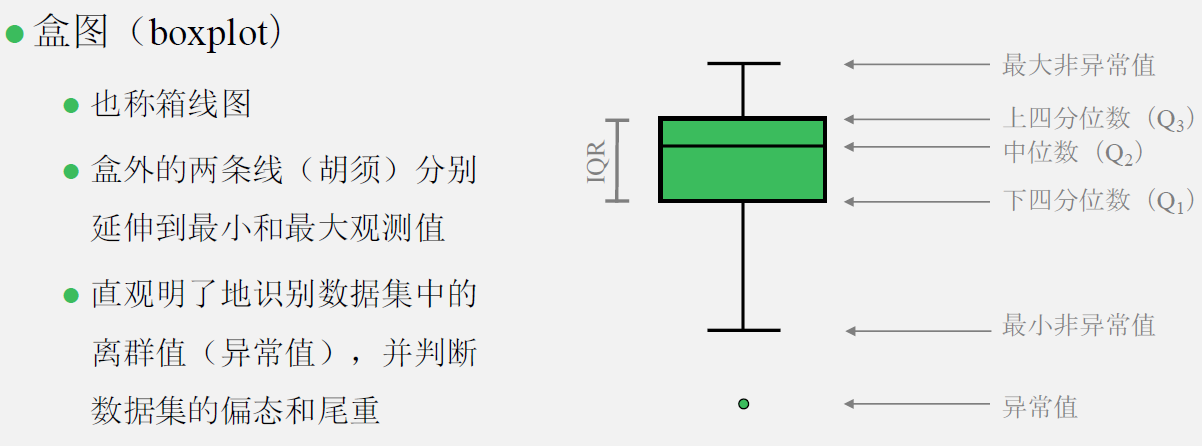
- 中间分位数(IQR): IQR = Q3 - Q1, 也叫四分位距,用来衡量数据的分散情况。
- 方差(Variance)和标准差(Standard deviation)
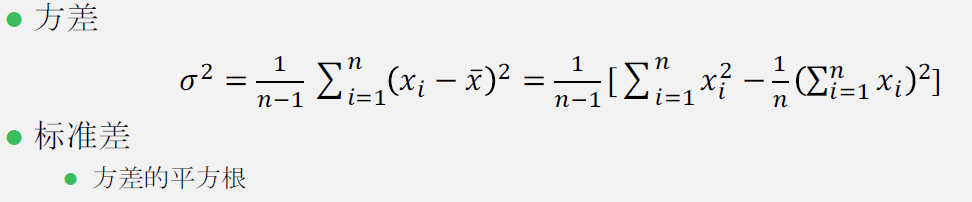
- 盒图(箱线图)
距离度量
相似性,值域通常为[0,1]
名义型数据类型 & 布尔型数据类型
- 简单匹配(相同属性个数m,属性数量p,则距离为p-m/p)
- 转换为多个布尔属性,如下图所示

q是两者都有的一个属性,r是i有但是j没有的属性。
数值型数据类型
明可夫斯基距离:

余弦相似度:

前者是绝对距离,后者是方向差异。
前者体现维度数值大小的差异,后者体现类似于用户兴趣之类的差异。
等级型数值类型

混合型数据类型
将上述的类型求得的距离进行加权求和。
数据预处理的方式
- 数据清洗
- 数据集成
- 数据转换
- 数据归约
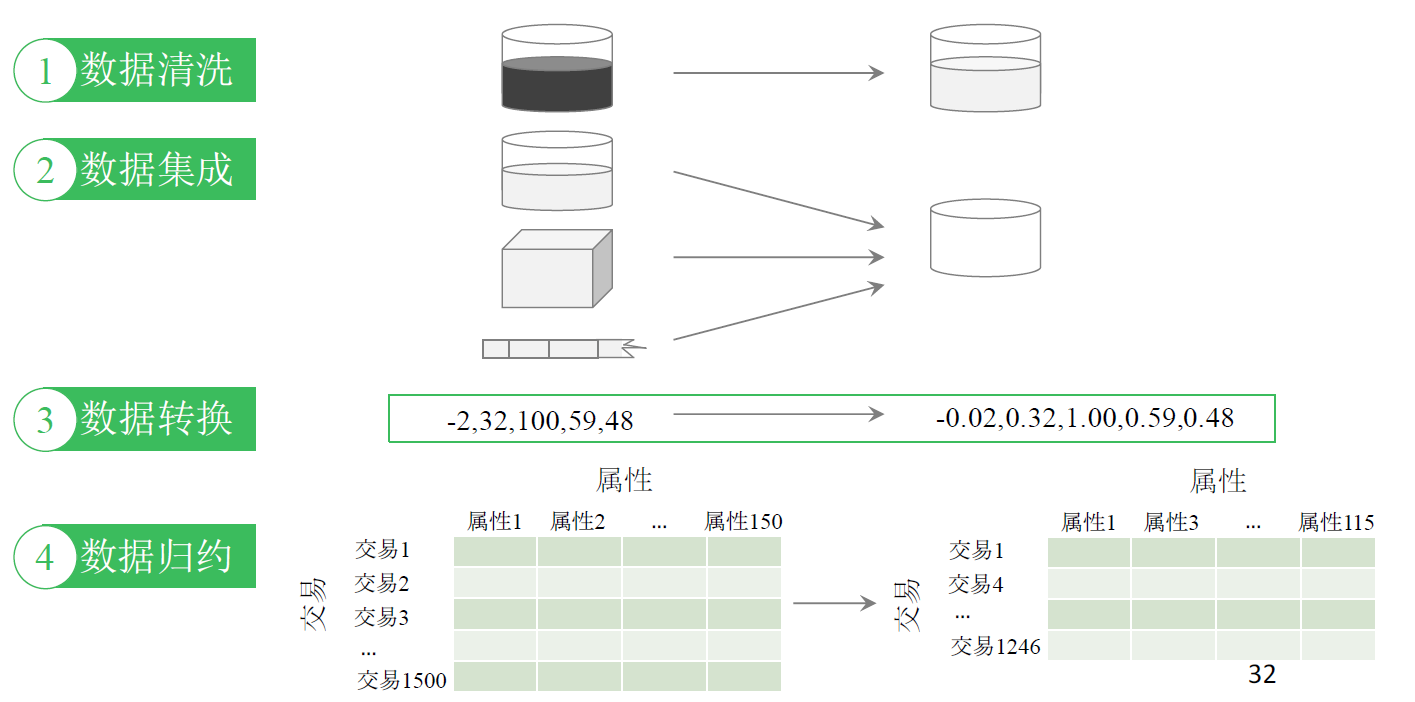
数据标准化
算法要求或者数据量纲不同:
- Z-score标准化:接近(0,1)分布,适用于最值未知
- 0-1标准化:线性变换到[0,1]区间
- 小数定标标准化:

- logistic标准化
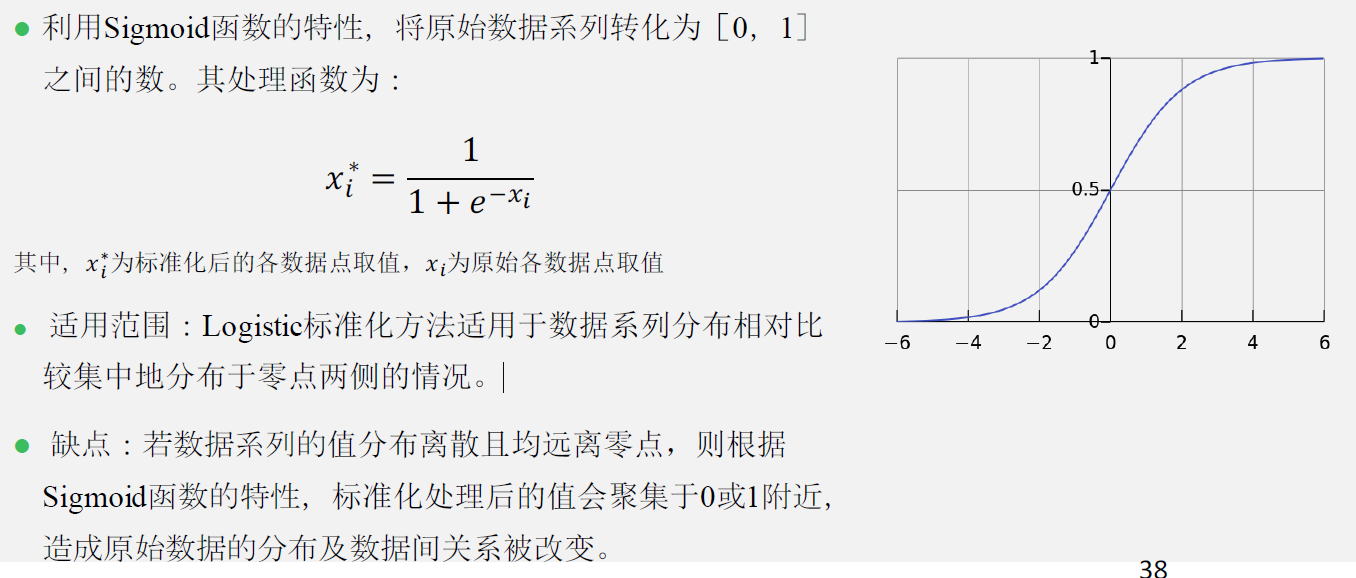
当数据集中的分布在零点附近时,通过sigmoid函数可以将其均匀地散开。
方法比较
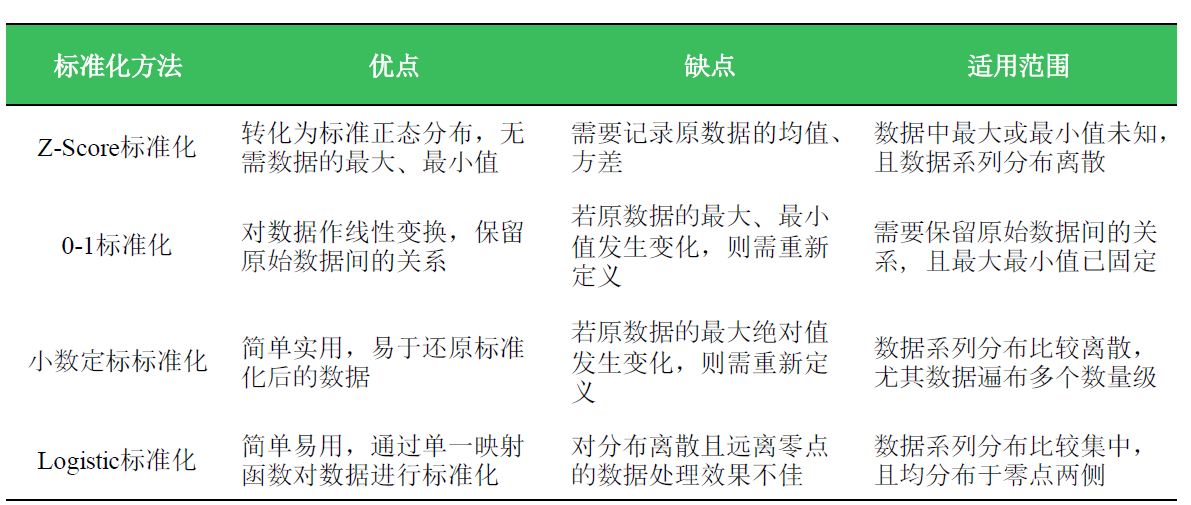
数据离散化
有些数据挖掘算法,特别是某些分类算法(如朴素贝叶斯),要求数据是分类属性形式(类别型属性)这样常常需要将连续属性变换成分类属性(离散化,Discretization)。另外,如果一个分类属性(或特征)具有大量不同值,或者某些之出现不频繁,则对于某些数据挖掘任务,通过合并某些值减少类别的数目可能是有益的。(具体可参考“离散化与稠密化”)
本质:将连续型数据分段
无监督离散化
- 等距离散化
- 等频离散化
- 基于聚类分析的离散化(先聚类,再合并(自底向上)或分裂(自顶向下),达到预定的簇个数)
- 基于正态3σ的离散化
- 有监督离散化
- 基于信息增益的离散化(自顶向下)
- 基于卡方的离散化(自底向上,根据不同区间的类分布相似度进行聚合,相似度越高,卡方值越小)
小结
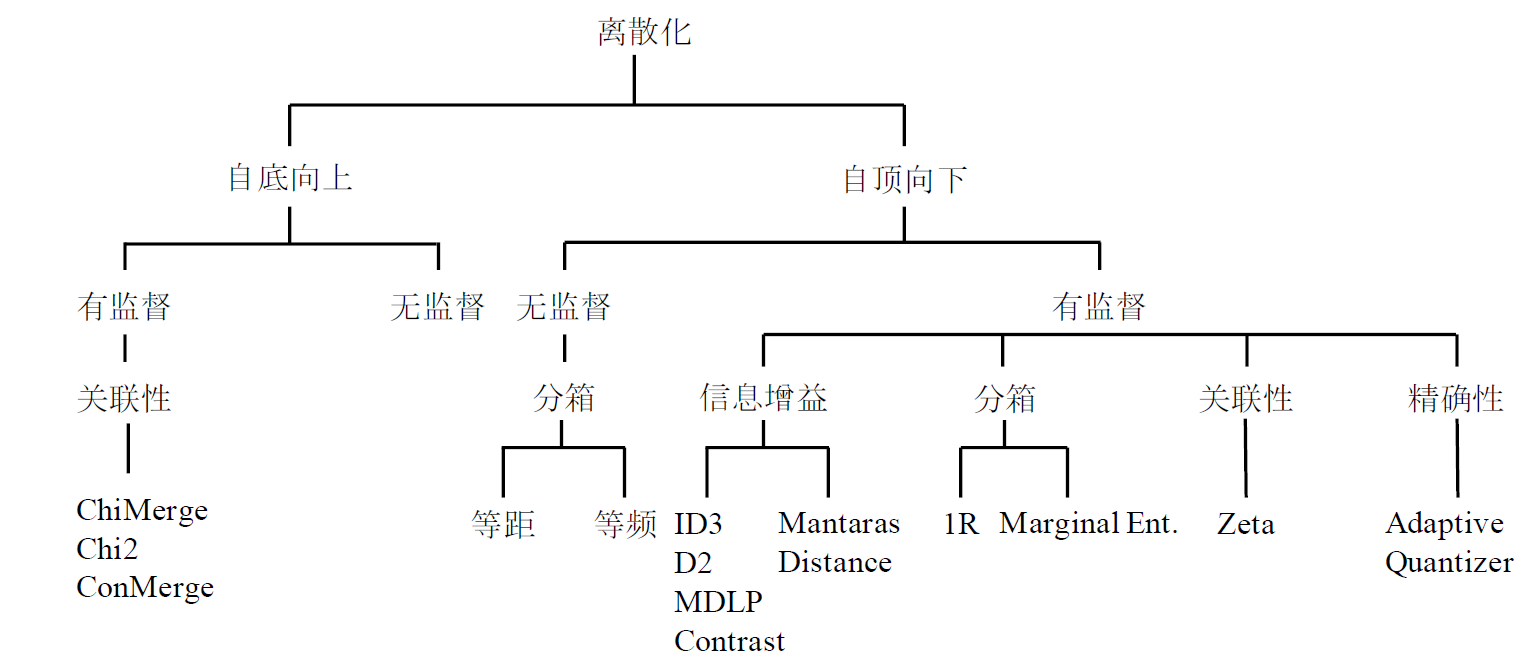
缺失值处理
缺失机制
- 完全随机缺失
- 随机缺失(与完全变量有关)
- 完全非随机缺失(与不完全变量自身有关)
处理方法
删除法
- 删除样本
- 删除变量(缺得多,对研究目标影响不大)
- 降低权重(不影响数据结构)
基于填补的方法
- 单一填补(均值、k-means、热平台、冷平台)
- 随机填补(在均值填补的基础上加随机项)
- 基于模型的方法
- 建模预测
异常值检测
基于统计的方法
上下α分位数之外的值
基于距离的算法
局部异常因子算法(LOF算法)